Can you pay too much taxes for SRS withdrawal?

When it comes to the Supplementary Retirement Scheme (SRS), four of the most common questions on forums and websites like Seedly and HardwareZone are the following:

"At what tax bracket would it make sense for me to contribute to my SRS account?"

"At what age should I start contributing to my SRS account?"

"How do I maximise tax savings yet minimise future tax expenses when I withdraw from my SRS account?"

"Should I keep my SRS account below $400,000 to get tax-free withdrawals?"

Before going into the weeds, let’s first recap what the SRS account does and how it is taxed.

How does taxation for SRS withdrawal work?

SRS account acts as a tax deferment account. You will get an equivalent amount in tax relief for every dollar of SRS contribution during the year of contribution. This contribution incentivises taxpayers to plan for retirement. However, any early SRS withdrawals will be subject to a 5% penalty and income tax. 

It is a voluntary scheme that helps you save on sizable taxes. SRS withdrawals at retirement age are still subject to income tax but at a preferential rate of 50% of the withdrawal amount. You can spread your withdrawals over 10 years to reduce income tax. The age when you can make preferential SRS withdrawal is tied to the retirement age when you first make an SRS contribution. 

For those aiming to reduce income tax, keeping an SRS account balance below $400,000 seems to make perfect sense, as your annual withdrawal of $40,000 will not be liable for income tax.

Understanding SRS top-up maximisation

Defining the SRS top-up problem

John is 35 years old this year and earning a modest income that puts him in the 7% tax bracket. He wants to maximise his income tax relief by utilising his SRS account, putting in the maximum of $15,300 for tax relief. 

He intends to withdraw his SRS account ten years past his retirement age. He assumes a 7% return on his investments. Would topping up his SRS account make him better off financially, assuming that income tax rates will not change?

The "Independent Variables" defining the SRS top-up problem

Moving ahead to secondary school maths (yes, I am cheating), the above Primary 6 problem sum can roughly be explained using dependent and independent variables.

J = ax+ by-cz

The independent variables, or the values x, y, and z in the above formula, are simple. These will be things like John's

1. Age (35 years old),
2. Tax bracket (7% tax bracket), and
3. Returns on investments (7% returns).

To make this analysis more straightforward, we will assume that figures like the $15,300 committed in SRS, and income tax rates are fixed numbers (or a, b, c in the above formula).

Understanding what we are maximising in SRS

The outcome we are optimising for is simply to grow our wealth at SRS withdrawal to the largest amount possible relative to not contributing to SRS. To achieve this, we have to consider the tax brackets, returns of investments, and the 10-year tax preference treatment of SRS withdrawals.

To ensure that an apples-for-apples comparison is made, let us assume that John is only willing to commit $15,300 of pre-tax savings to invest.

Fleshing out the workings for the dependent variable:

Let H - I = J where J is the upside (or downside when the value is negative) from investing through SRS rather than using post-tax monies, where:

H be 10-year yearly cash flow, net of taxes that John's SRS account will give him when he withdraws his SRS monies while staying invested

I be 10-year yearly cashflow, that John's post-tax cash account will provide him with.

For H, do note that since John is likely to have put a considerable sum of money in SRS, and given that it compounds at 7%, his portfolio would have grown to $1.14 million by 62.  Even though only 50% of the amount withdrawn from the SRS account is taxable, the sheer size of John's portfolio means he will be taxed.

Remember that if John paid his taxes, being in the 7% tax bracket, he would be left with $14,229 to invest in a portfolio with a 7% return over 26 years.

The worked sample solution for SRS maximisation

When John is 62, his SRS account will grow to $1.14 million. John will have a yearly cash flow of around $159,000 after taxes after liquidating his SRS account over 10 years.

If John were to invest using post-tax monies, John's portfolio would grow to $1.06 million. John will have a yearly cashflow of $151,000 investing with post-tax funds.

John (or value J) is better off by $8,000 (rounded up) a year just by investing through SRS instead of investing through post-tax monies.

What to consider before doing SRS top-ups

Your current tax bracket and contribution age

Of course, you are not John — your tax bracket is different, your age is different, and your expectations of investment returns are likely to differ. The easy part of solving maths problems in Excel rather than through paper and pen (as in the case of Primary 6 exams) is that we can use sensitivity tables for the analysis.

With a range of values for the independent variables, we can give you a personalised perspective of how SRS can work (or not work) for you. The sensitivity tables are as shown below (red highlights are cases where it does not work for you):

‍

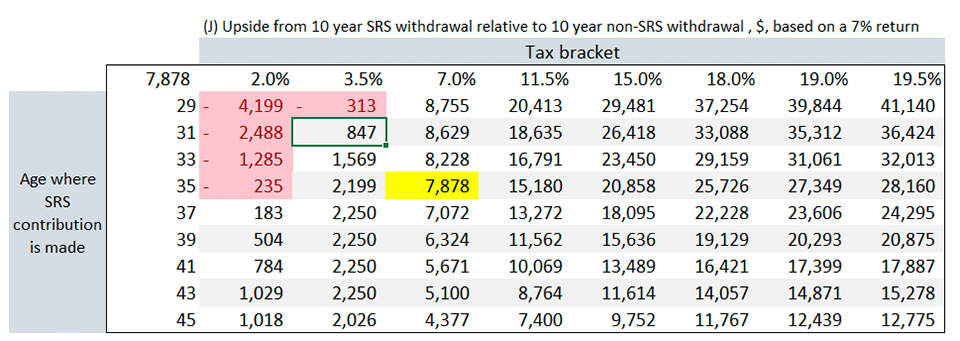
John's case (35-year-old, 7% tax bracket, 7% return) is highlighted in yellow above. As you can see from the above table, the higher your tax bracket, the more you save through SRS, even though you may be paying more taxes on an absolute basis. Just like how a dollar now is worth more than a dollar in the future, a tax dollar saved now is worth more than a tax dollar paid in the future.

Tax savings can be compounded and grown to pay for higher taxes in the future.

The age you start contributing to SRS matters as well.

See how starting at different ages affects the upside we can get from SRS. Starting later reduces your returns from SRS.

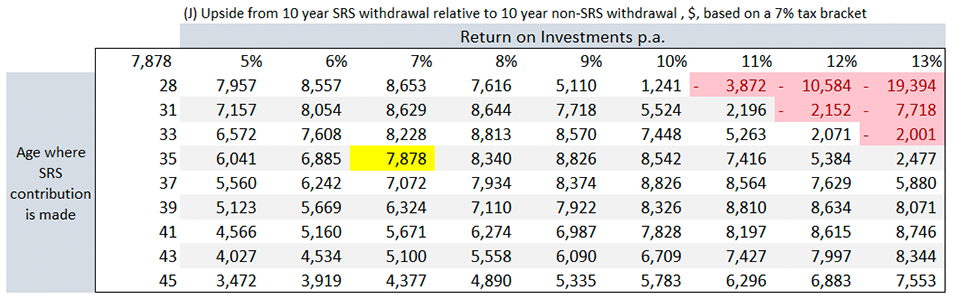
For returns, the higher returns are worse for you. The intuition behind it is straightforward. As the SRS account is a tax deferral scheme, if you expect a high investment return, it's better to be taxed now, grow your wealth significantly, and be taxed later.

Other concerns around SRS top-ups

Investing in your SRS is ultimately a long-term commitment where your funds are locked in until retirement age. There is a trade-off in terms of liquidity, and you must ensure that you do not need the money committed into the SRS account.

You should look at your medium to long-term significant ticket expenses (such as buying a new property or a new car, for example) before you commit to topping up your SRS account.

Note that we assume you have zero income at retirement, and any income tax payable will be solely from SRS withdrawals. If you earn property rental income in Singapore or still working part-time, this analysis will not apply to you. The recommendations here may not apply in those circumstances.

Conclusion

Generally, paying taxes from topping up SRS early and having your SRS account grow to a larger balance is not as big an issue as many would have imagined, as shown from our analysis above. Saving some tax now, and letting it compound till retirement even if you pay tax later still works well for growing your wealth.

If the analysis above makes sense to you, set up your SRS account or top it up now to reduce your taxable income. You can set up an account online and fund it immediately with local banks. We have a suite of SRS investment solutions available on Endowus that you can consider.

<divider><divider>

Investment involves risk. The value of investments and the income from them can go down as well as up, and you may not get the full amount you invested. Past performance is not an indicator nor a guarantee of future performance. Rates of exchange may cause the value of investments to go up or down. Individual stock performance does not represent the return of a fund. 

Any forward-looking statements, prediction, projection or forecast on the economy, stock market, bond market or economic trends of the markets contained in this material are subject to market influences and contingent upon matters outside the control of Endow.us Pte. Ltd (“Endowus”) and therefore may not be realised in the future. Further, any opinion or estimate is made on a general basis and subject to change without notice. In presenting the information above, none of Endowus Pte. Ltd., its affiliates, directors, employees, representatives or agents have given any consideration to, nor have made any investigation of the objective, financial situation or particular need of any user, reader, any specific person or group of persons. Therefore, no representation is made as to the completeness and adequacy of the information to make an informed decision. You should carefully consider (i) whether any investment views and products/ services are appropriate in view of your investment experience, objectives, financial resources and relevant circumstances. You may also wish to seek financial advice through a financial advisor or the Endowus platform and independent legal, accounting, regulatory or tax advice, as appropriate.